El Análisis de Clúster, también conocido como clustering o análisis de conglomerados, es una técnica multivariada y de aprendizaje no supervisado, que clasifica elementos en grupos homogéneos llamados clústeres o conglomerados; su objetivo principal es identificar estructuras o patrones naturales en los datos y organizar la información en categorías basadas en similitudes.
Este método es descriptivo y no inferencial por lo que no se realiza inferencias estadísticas mediante muestras, tampoco es necesario tener categorías predefinidas, convirtiéndolo en una herramienta exploratoria ideal para entender aquellos datos complejos. Para saber qué tan similares o diferentes son los elementos, utiliza criterios como la distancia euclidiana, correlación y selección de algoritmos de clasificación adecuados; los grupos obtenidos deben mostrar alta homogeneidad interna (los elementos dentro de un clúster son lo más similares posible) y gran heterogeneidad externa (los elementos entre clústeres son lo más diferentes posible); en contraste con otras técnicas como el análisis factorial que reduce el número de variables, el análisis de clúster, agrupa observaciones o casos.
El clustering permite identificar tendencias y validar hipótesis, las soluciones dependen del conjunto de variables y el método utilizado, lo que afecta significativamente a los resultados por lo que no siempre son definitivos; aun así, esta herramienta es útil para explorar e interpretar datos, encontrar patrones y apoyar decisiones informadas. Se utiliza ampliamente en muchas disciplinas como en marketing para segmentar clientes, en biología para clasificar genes, en investigación de mercados, en aprendizaje automático, en reconocimiento de patrones, etc.
¿QUÉ ES UN CLÚSTER?
Se llama clúster al conjunto de elementos u objetos que tienen características similares entre sí, pero que son diferentes a elementos de otros grupos; para el análisis de datos, los clústeres son subconjuntos de datos homogéneos agrupados por su similitud y distancia que están dentro de un conjunto de datos más grande, entonces, un clúster es una unidad formada por elementos más pequeños que tienen su propia identidad y que al agruparse, presentan características comunes que facilitan su clasificación y análisis.
TIPOS DE CLÚSTERES
Los tipos de clústeres se clasifican según las características de los datos y del enfoque de agrupamiento:
- Clústeres esféricos. Los elementos se agrupan uniformemente alrededor de un punto central, siguiendo un patrón circular; esto se puede observar en algoritmos K-Means.
- Elípticos. Son clústeres alargados que se extienden en distintas direcciones, normalmente se asocian a datos que no tienen una distribución uniforme y se pueden detectar mediante modelos como los Gaussian Mixture Models o GMM.
- Arbitrarios o no convexos. Estos clústeres tienen formas irregulares y complejas ya sean curvas o patrones no lineales, son detectados mediante DBSCAN y OPTICS.
- Clústeres superpuestos. Cuando la forma de los clústeres es difusa pues algunos elementos pertenecen a más de un clúster; se pueden reconocer utilizando técnicas de clustering difuso.
.
2. Según la densidad
- Densos. Los elementos en estos clústeres tienen una alta densidad en el espacio agrupándose de forma compacta, incluso cuando hay ruido; para su detección se utilizan los algoritmo basados en densidad como el DBSCAN.
- Dispersos. Los elementos en clústeres dispersos muestran una alta variabilidad; cuanto más dispersos están los datos, presentan una menor densidad, no obstante, los patrones son reconocibles y requieren de algoritmos que puedan manejar densidades bajas como el clustering jerárquico.
3. Según la naturaleza del clúster
- Homogéneos: Los elementos dentro de estos clústeres son muy similares, este patrón de agrupaciones es típico en los estudios de segmentación de mercados y en biología.
- Heterogéneos: Este tipo de clústeres presenta mayor variabilidad entre sus elementos, pero puede diferenciarse de otros clústeres.
4. Según el tamaño
- Clústeres equitativos: Todos los clústeres tienen tamaños muy similares, este tipo de clústeres suelen ser generados por K-Means.
- Clústeres desiguales: Cuando las agrupaciones de los datos son significativamente más grandes o más pequeñas que otros clústeres; puede verificarse con DBSCAN o clustering jerárquico, ya que no imponen restricciones.
5. Según el contexto de los datos
- Clústeres de objetos. En este caso, los clústeres son agrupaciones de personas, clientes, productos u otros objetos discretos, se usa mucho en segmentación de mercados.
- Clústeres de variables o atributos. Aquí, los clústeres son agrupaciones de características o atributos (en lugar de personas), puede observarse en investigación científica, determinando las relaciones entre diferentes variables.
- Clústeres temporales. se observan en clústeres de datos con componentes de temporalidad o en análisis de comportamientos a lo largo del tiempo (series temporales).
TIPOS DE ANÁLISIS DE CLUSTERING
1. Clustering jerárquico
En este tipo de clustering, la información está estructurada en un árbol jerárquico denominado dendrograma donde los datos se agrupan de forma secuencial, combinando elementos o formando subgrupos, además, no requiere especificar previamente el número de clústeres y usa medidas de similitud como la distancia euclidiana, llegando a ser caro computacionalmente cuando se trabaja con grandes conjuntos de datos; puede ser de dos tipos:
- Aglomerativo (Bottom-Up) que empieza con cada elemento como un clúster individual y los va agrupando.
- Divisivo (Top-Down) que empieza con un clúster grande y lo va dividiendo.
El clustering jerárquico puede ser útil en el acercamiento a las relaciones jerárquicas como puede ser en taxonomía biológica o en el análisis de datos genealógicos.
2. Clustering particional
Se dividen los datos en un número fijo de clústeres según un criterio determinado por el usuario, es eficiente en grandes conjuntos de datos y los algoritmos más comunes son K-Means (agrupación en función de centroide) y K-Medoids (función de Medoids o representantes de clústeres); es común en segmentación de clientes y en estudio de características socioeconómicas divididas por regiones geográficas.
3. Clustering basado en densidad
Agrupa aquellos datos que están densamente interconectados y separa los de baja densidad pues son considerados como ruido, no requiere especificar el número de clústeres e identifica clústeres de formas no convexas, el algoritmo que se usa habitualmente es el DBSCAN (Density-Based Spatial Clustering of Applications with Noise) y se aplica en la detección de anomalías o ruido en grandes conjuntos de datos y también en el reconocimiento de patrones de imágenes satelitales.
4. Clustering basado en modelos
Agrupa datos en función de probabilidades de pertenencia, asume que los datos se generan de un modelo probabilístico como las distribuciones gaussianas (p.e. modelos mezclados Gaussianos o Gaussian Mixture Models - GMM).
5. Clustering Difuso (Fuzzy Clustering)
En este tipo de clustering, un mismo dato puede pertenecer a más de un clúster pero con diferentes grados de pertenencia asignando probabilidades de pertenencia a cada clúster, resulta útil cuando los límites entre los clústeres son difusos o entrelazados; el algoritmo más utilizado es el Fuzzy C-Means. Puede utilizarse en la segmentación de imágenes o en la clasificación de consumidores con comportamientos superpuestos.
6. Clustering Basado en Grafos
Los datos se agrupan gráficamente en forma de nodos y conexiones (aristas) para encontrar comunidades o agrupamientos en redes, es útil para expresar las relaciones existentes entre elementos (p.e. en el análisis de redes sociales, en redes de transportes o en telecomunicaciones).
7. Clustering Basado en Restricciones
Agrupa datos en función de restricciones o reglas lógicas, basándose en información previamente conocida; se usa en análisis de decisiones o minería de datos.
8. Clustering Espectral
Se basa en el uso de algunas propiedades propias del álgebra lineal como matrices de similitud para dividir los datos en clústeres.
9. Clustering Incremental
Ajusta los clústeres conforme se disponga de nuevos datos, sin tener que volver a calcularlo todo desde cero.
FASES BÁSICAS DEL ANÁLISIS CLÚSTER
MEDIDAS DE SIMILARIDAD, DISTANCIA Y CORRELACIÓN
Para medir el grado de semejanza o diferencia entre puntos de datos (sean objetos o variables), la elección de su medición depende del tipo de datos y del objetivo del análisis; las medidas o técnicas de distancias, cuantifican las diferencias entre puntos de datos, entre las más comunes tenemos las distancias euclidiana, Manhattan, Minckowski, coseno, entre otras; las medidas de similitud que miden cuánto se parecen dos objetos entre sí, presentan técnicas como coeficiente de Jaccard, Dice, Hamming, entre otras; por otra parte, la correlación mide la relación entre dos variables, teniendo técnicas como correlación de Pearson, Spearman y Kendall, en la siguiente tabla se observan algunas características:
| Técnica | Tipo de Datos | Características | Usos Principales | Fórmula |
| Distancia Euclidiana | Numérico | Mide la distancia más corta entre dos puntos, es sensible a las escalas de las variables y a los valores atípicos. | Clustering K-Means, K-Nearest Neighbors, análisis geométrico, etc. |
|
| Distancia de Manhattan | Numérico | Suma de las distancias absolutas, funciona para datos con trayectorias ortogonales y es resistente a valores atípicos. | Geolocalización, análisis de redes, datos discretos, etc. |
|
| Distancia de Minkowski | Numérico | Generaliza técnicas Euclidiana y Manhattan con un parámetro p. | Algoritmos con flexibilidad en métricas. |
|
| Distancia Chebyshev | Numérico | Máxima distancia entre las coordenadas de dos puntos. | Optimización, clustering de datos con restricciones. |
|
| Distancia de Mahalanobis | Numéricos (multivariados) | Consideran correlaciones entre variables, requiere matriz de covarianza invertible. | Análisis discriminante y detección de valores atípicos. |
|
| Distancia Bray-Curtis | Numéricos (proporciones) | Mide las diferencias entre dos muestras en proporción al total de sus valores. | Ecología, análisis de comunidades biológicas. |
|
| Distancia Coseno | Vectores, textos | Mide el ángulo entre dos vectores sin considerar su magnitud, presenta valores entre -1 y 1 (donde 1 es la máxima similitud) | Procesamiento de lenguaje natural, análisis de documentos, vectores de caracterización, etc. |
|
| Coeficiente de Jaccard | Binarios, categóricos | Razón entre la intersección y la unión de dos conjuntos, no es muy recomendable para conjuntos muy grandes. | Bioinformática, análisis de presencia/ausencia. |
|
| Similitud de Dice | Binarios, categóricos | Variante de Jaccard que enfatiza la intersección, pero es más sensible a conjuntos muy pequeños. | Comparación de conjuntos en biología, análisis de similitud de texto. |
|
| Distancia de Hamming | Binarios, categóricos | Mide la proporción de posiciones iguales en dos cadenas binarias. | Análisis de ADN, clasificación de cadenas binarias. |
|
| Correlación de Pearson | Numéricos contínuos | Evalúa la relación lineal entre dos variables, toma valores entre -1 y 1. | Análisis de asociaciones lineales, regresión lineal. |
|
| Correlación de Spearman | Numéricos (rangos), ordinales | Mide relaciones monotónicas utilizando rangos en lugar de valores originales. | Datos ordinales, variables con relaciones no lineales. |
|
| Correlación de Kendall | Ordinales | Basada en concordancias/discordancias entre pares de datos, adecuada para conjuntos pequeños. | Análisis de clasificaciones, preferencias de usuarios. |
ALGORITMOS DE CLUSTERING, SEGÚN MÉTODOS.
Según OpenAI, los algoritmos de clustering se encuentran distribuidos por métodos o tipos, de la siguiente forma:
- MiniBatch K-means: Es una variante de K-means para trabajar con pequeños grupos de datos y reducir el tiempo de cómputo.
- K-medoids: Es similar a K-Means, pero utiliza un punto real como centroide o medoide, es más robusto frente a valores atípicos.
- PAM (Partitioning Around Medoids): Extensión de K-Medoids, que optimiza la selección de los medoides.
- CLARA (Clustering Large Applications): K-medoids para manejar grandes grupos de datos mediante muestras representativas, con el objetivo de reducir el tiempo de cómputo.
- CLARANS (Clustering Large Applications based on Randomized Search): K-Medoids para grandes bases de datos.
- Fuzzy C-means (FCM). Permite que un punto pertenezca a varios clústeres con distintos "grados de pertenencia", se utiliza en análisis donde los límites entre grupos no están claros.
Enlace simple (Single Linkage). Usa la distrancia mas corta para unir clústeres.
* Enlace completo (Complete Linkage). Usa la distancia más larga entre puntos.
* Enlace promedio (Average linkage). Usa la distancia media entre sus puntos para unir clústeres.
* Ward’s Method. Minimiza la varianza total dentro de los clústeres.
- Divisivo o Divisive Hierarchical Clustering (DIANA). Inicia con todos los datos en un sólo clúster y los divide sucesivamente.
- Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH). Diseñado para grandes conjuntos de datos, crea una estructura de árbol para realizar clustering jerárquico.
- Robust Clustering using Links (ROCK). Realiza agrupamiento jerárquico aglomerativo y explora el concepto de enlaces para datos con atributos categóricos.
- Ordering Points To Identify the Clustering Structure (OPTICS). Similar a DBSCAN pero maneja clústeres con densidad variable.
- Hierarchical DBSCAN (HDBSCAN). Versión jerárquica de DBSCAN que construye un árbol de densidad.
- Density-based Clustering (DENCLUE). Utiliza funciones de densidad continua para identificar clústeres. .
- Mean Shift Clustering. Método no paramétrico que encuentra regiones densas de datos, para segmentación y seguimiento de objetos.
- Bayesian Clustering. Similar a GMM pero incorpora distribuciones previas para modelar incertidumbre.
- Hidden Markov Models (HMM). Usa modelos probabilísticos para identificar patrones en datos secuenciales, útil para reconocimiento de voz y series temporales.
- Dirichlet Process Clustering. Es una variante no paramétrica de GMM que permite determinar automáticamente el número de clústeres.
- Latent Dirichlet Allocation (LDA). Modelo probabilístico que sirve para identificar temas en un conjunto de documentos, pues agrupa palabras relacionadas en tópicos, útil en análisis de texto y minería de temas.
- Expectation-Maximization Algorithm (EM). Algoritmo iterativo del clustering probabilístico para estimar parámetros de modelos estadísticos en presencia de datos incompletos.
- Markov Clustering (MCL). Simula flujos aleatorios en un grafo para identificar grupos densamente conectados, ideal para redes biológicas.
- Girvan-Newman: Elimina iterativamente las aristas más centrales para dividir el grafo.
- Walktrap: Detecta comunidades mediante simulaciones de caminatas aleatorias.
- Louvain Method: Optimiza la modularidad del grafo.
- Clique Percolation Method: Detecta cliques o camarillas superpuestas en redes.
- Chinese Whispers Algorithm. Algoritmo de clustering para grafos basado en la propagación de etiquetas entre nodos adyacentes, sea aplica en la detección de comunidades en redes sociales.
- Clustering In Quest (CLIQUE). Combina clustering basado en densidad y rejilla para datos multidimensionales y es útil para datos de alta dimensión.
- WaveCluster. Usa transformadas de onda para identificar clústeres en datos espaciales útil para análisis de imágenes y datos espaciales.
- OPTGRID. Algoritmo basado en grillas que optimiza la partición de datos espaciales mediante densidades locales.
- Particle Swarm Optimization (PSO) para Clustering. Basado en la optimización por enjambre de partículas o comportamientos colectivos, simula el comportamiento de enjambres para agrupar datos, resulta rápido en problemas grandes.
- Simulated Annealing Clustering: Optimización basada en procesos térmicos.
- Ant Colony Optimization (ACO). Algoritmo que está inspirado en el comportamiento de las hormigas, encuentra clústeres optimizando rutas basadas en feromonas virtuales, puede ser utilizado en análisis de clustering dinámico y problemas combinatorios.
- Simulated Annealing para Clustering. Técnica de optimización para grandes conjuntos de datos que simula el enfriamiento gradual de un material para encontrar la mejor agrupación posible.
- Shared Nearest Neighbor Clustering (SNN). Agrupa puntos que comparten vecinos comunes.
- Agglomerative Clustering (AHC). Método jerárquico que inicia con cada punto como un clúster separado y los combina en grupos más grandes basados en similitudes, útil en segmentación de mercados.
-Clustering Using Representatives (CURE). Combina representaciones dispersas de clústeres para manejar formas no esféricas y valores atípicos.
- PCKmeans: Permite priorizar algunas restricciones más que otras.
- Semi-supervised K-Means: Variante de K-Means que incorpora restricciones de "must-link" y "cannot-link".
- Gustafson-Kessel Algorithm. Variante del Fuzzy C-Means, adapta las formas de los clústeres al estimar matrices de covarianza locales, permitiendo clústeres elípticos, útil para clasificación de patrones y modelado en sistemas dinámicos.
- Fuzzy Clustering with Quadratic Regularization. Modifica Fuzzy C-Means con términos de regularización para manejar ruido y valores atípicos.
- Fuzzy Relational Clustering. En lugar de trabajar directamente con las coordenadas de los datos, utiliza matrices de relación o similitud, ideal para datos relacionales o no estructurados.
- Possibilistic C-Means (PCM). Modificación del Fuzzy C-Means donde el grado de pertenencia se basa en una interpretación posibilística, eliminando la necesidad de que las pertenencias sumen 1, no requiere normalización de los grados de pertenencia.
- Fuzzy Subtractive Clustering. Identifica automáticamente los centros de clústeres calculando la densidad de puntos en el espacio de datos.
- Intuitionistic Fuzzy Clustering. Extensión de Fuzzy Clustering que considera no solo el grado de pertenencia, sino también un grado de no pertenencia y un grado de incertidumbre a fin de manejar mejor la ambigüedad en los datos, utilizado comúnmente en toma de decisiones en entornos inciertos e inteligencia artificial.
- MapReduce-based Clustering: Utiliza el paradigma MapReduce para agrupar datos masivos.
- BigData Clustering. Métodos diseñados para procesar grandes volúmenes de datos, como Apache Mahout y Spark MLlib.
- DenStream: Variante de DBSCAN para datos en streaming.
- Non-Negative Matrix Factorization (NMF): Descompone la matriz de datos para encontrar patrones subyacentes
- Autoencoder Clustering: Utiliza redes neuronales para reducir la dimensionalidad y realizar agrupamiento en el espacio latente.
- Deep Embedded Clustering (DEC). Combina autoencoders con clustering al analizar datos no lineales.
- Variational Autoencoders for Clustering (VAE): Utiliza modelos probabilísticos latentes para identificar clústeres.
- Convolutional Clustering: Aplica clustering a imágenes mediante redes convolucionales.
- SpectralNet: Combina aprendizaje profundo con clustering espectral.
- Kohonen Maps. Redes neuronales autoorganizadas para agrupar y visualizar datos.
- Infomap. Se basa en mapas de flujo y se usa en análisis de redes, para identificar comunidades en grafos.
- Edge Betweenness. Divide grafos al eliminar aristas de alta intermediación, es útil en análisis de redes sociales y biológicas.
- Label Propagation. Clustering rápido basado en la propagación de etiquetas a través de grafos, usado en redes dinámicas
- StreamKM++. Variante de K-means para flujos de datos masivos, se utiliza comúnmente en streaming en tiempo real.
- CluStream. Diseñado para datos en flujo continuo que divide a los datos en microclústeres temporales, útil para monitoreo en tiempo real.
- DenStream. Extiende DBSCAN para manejar datos dinámicos.
- SOStream (Self-Organizing Stream Clustering). Clustering autoorganizado para datos en flujo continuo por ejemplo para detección de anomalías.
- Subspace Clustering (SUBCLU). Identifica clústeres en subespacios de alta dimensión.
- Projected Clustering (PROCLUS). En datos heterogéneos, encuentra clústeres en subespacios seleccionados.
- COOLCAT. Clustering basado en minimizar la entropía dentro de los clústeres, usado para datos categóricos.
- High Contrast Subspaces (HiCS). Detecta clústeres contrastantes en subespacios de datos de alta dimensión, puede ser aplicado en bioinformática y minería de datos.
- Hierarchical Clustering para texto. Organiza documentos en una jerarquía basada en similitudes textuales.
- Word2Vec Clustering. Agrupa palabras según sus vectores semánticos en Word2Vec para el procesamiento del lenguaje natural.
- TextRank. Algoritmo de grafo para extraer palabras clave y resumir textos
- Latent Semantic Analysis (LSA). Encuentra temas ocultos en datos textuales mediante descomposición matricial, útil para al recuperación de información.
- Robust PCA with Clustering. Combina reducción de dimensionalidad con resistencia a ruido.
- Multi-View Clustering. Combina múltiples conjuntos de características para realizar el clustering, integra información de varias vistas permitiendo manejar datos heterogéneos.
- Spectral Multi-View Clustering. Combina información espectral de varias vistas para agrupar los datos, reduce dimensionalidad antes del clustering utilizando matrices de similitud de cada vista.
- Ensemble Clustering. Combina resultados de múltiples algoritmos de clustering para generar un modelo final, ofrece mayor robustez frente al ruido y datos complejos, requiere algoritmos base diferentes.
- Multi-Representation Clustering. Extiende el clustering para considerar diferentes representaciones de datos (como transformaciones o proyecciones), integra diferentes dominios de características y puede manejar datos faltantes o incompletos.
- GDBSCAN: Mezcla densidad y partición para datos con ruido.
- Spectral-DBSCAN: Usa representaciones espectrales antes de aplicar DBSCAN.
- GMM-DBSCAN: Detecta densidades con DBSCAN y ajusta clústeres gaussianos.
En la siguiente tabla, se muestran las caracteríticas de algunos algoritmos de clustering más usados:
OPTIMIZACIÓN DE PARÁMETROS
Las técnicas de optimización de parámetros son aquellas que sirven para ajustar los valores de un modelo, así como para potenciar su rendimiento, incluyen número de clústeres, valores de umbral y métricas de distancia; algunas técnicas son:
- Método del codo (Elbow Method). Para determinar el número óptimo de clústeres se analiza el crecimiento gradual del número de clústeres a medida que la inercia (suma de distancias cuadradas que hay entre los puntos de datos y su centroide) se estabiliza.
- Coeficiente de silueta (Silhouette). Este coeficiente estudia el nivel de separación de los clústeres, un alto valor en el coeficiente indica que los clústeres son compactos y están bien separados.
- Grid Search. Se encarga de ajustar del tamaño del mínimo de clústeres para determinar la mejor combinación de parámetros.
- Random Search. Permite de manera aleatoria, seleccionar las combinaciones de parámetros dentro de un rango para evaluar su rendimiento.
- Validación interna y externa. Compara diferentes configuraciones para ajustar parámetros ya conocidos o que tienen etiquetas.
- Métodos basados en Heurísticas o Metaheurísticas. Busca la optimización de clustering avanzado o híbridos, aplicando algoritmos de procesos naturales, por ejemplo, algoritmos genéticos, PSO (optimización por enjambre de partículas), Simulated annealing, etc.
- Reducción de dimensionalidad previa. La reducción de una posible dimensionalidad previa, podría contribuir a un mejor rendimiento del algoritmo y también a reducir el número de parámetros.
- Optimización Bayesiana. Permite maximizar la predicción con respecto al rendimiento del modelo, utilizando modelos probabilísticos con diferentes combinaciones de parámetros.
- Validación cruzada. Divide la muestra en subconjuntos o folds, evaluando el modelo en cada uno de los subconjuntos y eligiendo parámetros que tengan un mejor equilibrio entre subajuste y sobreajuste; es una técnica muy utilizada en modelo supervisados, pero puede adaptarse al clustering para evaluar las métricas internas..
TÉCNICAS DE REDUCCIÓN DE DIMENSIONALIDAD
Estas técnicas permiten reducir dimensiones manteniendo, en lo posible, información relevante; ayuda a simplificar el análisis al reducir ruido, mejorando el desempeño de los algoritmos y facilitando la visualización de los datos; para seleccionar una técnica adecuada se considera la naturaleza de los datos y el propósito del análisis, entre estas técnicas, tenemos algunas:
- Análisis de Componentes Principales (PCA). Ordena los componentes principales según su importancia, seleccionando los mas significativos y maximizando la varianza explicada en cada eje o componente principal.
- Análisis de Componentes Independientes (ICA). Separa los datos en componentes estadísticamente independientes, buscando señales no correlacionadas; se puede utilizar en procesamiento de señales como EEG o audio y en el reconocimiento de patrones de datos complejos.
- Incrustación de Vecinos Estocásticos t-distribuida (t-SNE). Convierte datos de alta dimensionalidad en un espacio de baja dimensión preservando relaciones locales, es no lineal y es útil para visualización de datos complejos como genética o modelos de aprendizaje profundo.
- Aproximación y Proyección Uniforme de Manifold (UMAP). Preserva tanto relaciones locales como globales en los datos al reducir dimensiones; es más rápido que t-SNE y es útil para análisis exploratorio y visualización de grandes conjuntos de datos.
- Factorización de Matrices (NMF). Descompone una matriz en factores no negativos es útil para datos que no tienen valores negativos como frecuencias o probabilidades, se usa en minería de texto, análisis de temas y sistemas de filtrado colaborativo.- Autoencoders. Son redes neuronales entrenadas para comprimir y reconstruir datos aprendiendo representaciones latentes de menor dimensionalidad, es no lineal y altamente flexible, requiere de data grande para entrenar, comúnmente se usa en reducción de dimensionalidad de imágenes, series temporales, entre otros.
- Basado en Varianza. Selecciona variables que tienen mayor variación en el conjunto de datos eliminando aquellas con variación baja.
- Análisis de Correspondencias (CA). Técnica de reducción de dimensionalidad para datos categóricos, basada en el análisis de tablas de contingencia, representa las relaciones entre filas y columnas en un espacio reducido.
- Clustering Espacial. Simplifica datos geoespaciales al encontrar regiones similares en características reduciendo redundancias; utiliza información espacial para preservar la topología del conjunto de datos y es útil para el análisis de mapas y datos espaciales.
1. Validación Interna
Son técnicas que evalúan la calidad de los clúster utilizando sólo datos internos del clustering, sin considerar información externa.
a) Índice de Silueta. Mide la agrupación de los datos en un clúster comparado con los demás clústeres, es útil para evaluar cohesión y separación, no es recomendable usar en clústeres con formas irregulares o tamaños desiguales.
\[S(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}\]
Donde:
\(𝑎(𝑖)\): Distancia promedio entre el punto \(i\) y los demás puntos de su clúster.
\(𝑏(𝑖)\): Distancia promedio entre el punto \(i\) y los puntos del clúster más cercano.
\(𝑠(𝑖)\): Rango entre −1 y 1; valores cercanos a 1 indican buen clustering y cercanos a -1 mala asignación del punto en el cluster.
b) Índice de Dunn. Mide la relación entre la distancia mínima de los clústeres con el diámetro máximo dentro de los clústeres, considera separación y cohesión, es poco recomendable para datas grandes, pues el calculo se torna exhaustivo.
\[D = \frac{\min_{1 \leq i < j \leq k} \delta(C_i, C_j)}{\max_{1 \leq h \leq k} \Delta(C_h)}\]
Donde:\(\delta(C_i, C_j)\): Distancia mínima entre elementos de los clústeres \(𝐶_𝑖\) y \(𝐶_𝑗\).
\(\Delta(C_h)\): Diámetro del clúster \(C_h\) (distancia máxima entre dos puntos dentro de \(C_h\)).
c) Índice de Calinski-Harabasz. Relación entre la dispersión total entre clústeres y la dispersión dentro de los clústeres, es bueno con datos compactos y bien separados, sin embargo, es sensible a distribuciones desiguales o outliers.
\[CH = \frac{\text{Tr}(B_k)}{\text{Tr}(W_k)} \cdot \frac{n-k}{k-1}\]
Donde:
\(\text{Tr}(B_k)\): Suma de cuadrados entre los clústeres.
\(\text{Tr}(W_k)\): Suma de cuadrados dentro de los clústeres.
\(n\): Número total de observaciones.
\(k\): Número de clústeres.
d) Índice de Davies-Bouldin. Es el promedio de la relación entre la dispersión interna de los clústeres y su separación respecto a otros clústeres, valores bajos indican mejor calidad de clustering; puede resultar menos eficiente con clústeres de formas irregulares o tamaños desiguales.
\[DB = \frac{1}{k} \sum_{i=1}^{k} \max_{j \neq i} \frac{\sigma_i + \sigma_j}{d(C_i, C_j)}\]
Donde:
\(\sigma_i\): Dispersión del clúster \(i\) (distancia promedio entre los puntos y su centroide).
\(d(C_i, C_j)\): Distancia entre los centroides de los clústeres \(C_i\) y \(C_j\).
e) Varianza intra/inter clúster. Mide la homogeneidad dentro de los clústeres y la heterogeneidad entre ellos, se calcula mediante la suma de distancias cuadradas dentro y entre clústeres, es útil para maximizar diferencias entre clústeres.
f) Cohesión y Separación. Mide la cercanía entre los datos dentro de un clúster y la lejanía entre clústeres, evalúa datas pequeñas y medianas, sin embargo, es menos efectiva en presencia de datos ruidosos o de alta dimensionalidad.
2. Validación Externa
Comparan los clústeres obtenidos con etiquetas reales (clasificación preexistente).
a) Índice de Rand Ajustado (Adjusted Rand Index - ARI). Compara resultados de clustering con clasificaciones conocidas, ajustando según azar.
\[ARI = \frac{RI - E(RI)}{\max(RI) - E(RI)}\]
Donde:
\(ARI=1\): concordacia perfecta.:
\(ARI=0\): concordancia aleatoria.:
\(RI\):Concordancia entre dos particiones.
\(E(RI)\): Concordancia esperada por el azar.
b) Información Mutua Normalizada (NMI). Mide la cantidad de información compartida entre particiones generadas y reales.
\[ NMI = \frac{2 \cdot I(U;V)}{H(U) + H(V)}\]
Donde:\(I(U;V)\): Información mutua entre las particiones \(U\) y \(V\).
\(H(U)\): Entropía de la partición \(U\).
\(H(V)\): Entropía de la partición \(V\).
c) Matriz de confusión y precisión. Mide la coincidencia entre clústeres generados con etiquetas reales, usa métricas como precisión, recall y F1-Score.
3. Validación Relativa.
Comparan diferentes configuraciones de clustering.
a) Criterio del Codo. Identifica el número óptimo de clústeres donde la reducción de varianza comienza a estabilizarse, se grafica la suma de distancias intra-cluster (inercia), frente al número de clústeres.
\[\text{Inercia} = \sum_{i=1}^{k} \sum_{x \in C_i} ||x - \mu_i||^2\]
Donde:
\(C_i\): Clúster \(i\).
\(\mu_i\): Centroide del clúster
\(k\): Número de clústeres donde la disminución en la inercia empieza a estabilizarse.
b) Índice de Silueta Promedio. Evalúa la calidad del conglomerado considerando la selección del número optimo de clústeres basándose en la silueta promedio, toma valores entre -1 y 1.
c) Validación Cruzada. Divide el conjunto de datos en partes a fin de evaluar la estabilidad y generalización del clustering, valorando la robustez del modelo.
d) Bootstraping. Evalúa la estabilidad de los clústeres realizando particiones a partir de re-muestreos de los datos, se centra en la creación de modelos de conjunto y en la estimación de parámetros, puede resultar costoso computacionalmente al requerir muchos re-muestreos.
APLICACIONES DEL CLUSTERING
- Educación: Personalización del aprendizaje, estudios de deserción escolar, análisis de centros escolares, etc.
- Medio ambiente: Conservación de especies, clasificación de contaminantes, monocultivo de ecosistemas.
- Agricultura: Segmentación de cultivos, optimización de insumos, análisis de plagas, etc.
- Industria y manufactura: Mantenimiento predictivo, optimización de procesos, etc.
- Transporte y logística: Agrupación de trayectorias, segmentación de pasajeros, mantenimiento predictivo de vehículos, etc.
- Biología: Estudio de especies, análisis de proteínas, clasificación de genes, etc.
- Comercio Electrónico: Segmentación de productos, análisis de preferencias, agrupación de proveedores.
- Marketing: Segmentación de consumidores, diseño publicitarios, análisis de satisfacción, etc.
- Entre otras aplicaciones.
En conclusión, el clustering o análisis de conglomerados se caracteriza como una técnica de investigación de datos de tipo estadístico y de minería de datos muy potente que nos permite describir e interpretar datos mediante el agrupamiento en base a ciertas características o también similitudes; en función de ello, se podrían descubrir patrones, hacer predicciones y tomar decisiones sobre diversas áreas de aplicación.
Referencias: (1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13).










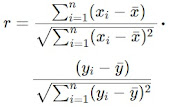










No hay comentarios:
Publicar un comentario