El juego de las Torres de Hanói es un dispositivo que consta de tres varillas verticales A, B y C y un número variable de discos. Los n discos son todos de diferente tamaño y, en la posición de partida del juego, todos los discos están colocados en la varilla A ordenados de mayor a menor tamaño, esto es, el mayor en el lugar más bajo y el menor arriba. El juego consiste en pasar todos los discos a la tercera varilla colocándolos de mayor a menor. Conforme aumenta el número de discos la dificultad del juego también, así como el tiempo de resolución sin haber cometido ningún error.
Leyenda
En las instrucciones que acompañaban al juego original, Édouard Lucas incluía una breve referencia a una leyenda relacionada con los brahmanes de Benarés (India) y sus templos: “En el gran templo de Benarés, debajo de la cúpula que marca el centro del mundo, yace una base de bronce, en donde se encuentran acomodadas tres agujas de diamante, cada una del grueso del cuerpo de una abeja y de una altura de 50 cm aproximadamente. En una de estas agujas, Dios, en el momento de la Creación, colocó sesenta y cuatro discos de oro, el mayor sobre la base de bronce y el resto de menor tamaño conforme se va ascendiendo. Día y noche, incesantemente, los sacerdotes del templo se turnan en el trabajo de mover los discos de una aguja a otra de acuerdo con las leyes impuestas e inmutables de Brahma, que requieren que siempre haya algún sacerdote trabajando, que no muevan más de un disco a la vez y que deben colocar cada disco en alguna de las agujas de modo que no cubra a un disco de radio menor. Cuando los sesenta y cuatro discos hayan sido transferidos de la aguja en la que Dios los colocó en el momento de la Creación a otra aguja, el templo y los brahmanes se convertirán en polvo y, junto con ellos, el mundo desaparecerá”. De ahí que a las Torres de Hanói también se le conoce como “Las torres de Brahma” o “El problema del fin del mundo”.
Notación
Se ordenarán tres varillas alineadas de izquierda a derecha y serán marcadas con letras mayúsculas A, B y C, el origen será A y el destino C y la varilla auxiliar B. Así mismo, los discos serán ordenados según el tamaño de su radio, estando el mayor en la base de la torre, para que se numeren de 1 a n, empezando por el más pequeño. Por ejemplo para ocho discos tenemos:
Reglas
El juego consiste en pasar todos los discos de la varilla A (origen) a la varilla C (destino), para lograrlo se deberá usar la varilla B (auxiliar). Para realizar este objetivo, es necesario seguir tres simples reglas:
- Sólo se puede mover un disco cada vez.
- Un disco de mayor tamaño no puede descansar sobre uno más pequeño que él mismo.
- Sólo se puede desplazar el disco que se encuentra arriba de cada varilla.
Solución
El juego se complica a medida que se agregan discos (el número de movimientos para resolver el problema crece exponencialmente conforme aumenta el número de discos), es así que para 3 discos utilizaremos primero la varilla C como auxiliar para colocar los dos primeros discos en B (movimientos 1, 2 y 3), luego llevaremos el tercer disco a C (movimiento 4), para finalmente usar la varilla A como auxiliar y llevar los dos discos que faltan a la varilla C (movimientos 5, 6 y 7). En total 7 movimientos.
Siguiendo la misma metodología el número de movimientos necesario para pasar 4 discos de mayor a menor diámetro de una varilla a otra sería: Total movimientos= 15.
De los resultados expuestos se puede deducir que el número de movimientos sigue la secuencia 1, 3, 7, 15,… para 1, 2, 3 y 4,… discos, y además se precisa colocar en la varilla de apoyo o auxiliar 0, 1, 2, 3,… discos respectivamente.
Se trata, pues, de un proceso iterativo para el que se puede establecer la siguiente regla: “En general, para mover ‘n’ discos de A a C son necesarios mínimamente 2ⁿ – 1 movimientos o también el número de movimientos necesarios para una cantidad de discos determinada es el doble de la cantidad anterior más uno”. En consecuencia, la función recursiva que nos da la expresión del número de movimientos del problema de las Torres de Hanói es:
A continuación se muestra en la tabla, la progresión geométrica del número de movimientos mínimos requeridos para resolver las torres de Hanói según la cantidad de discos, así como la comparación con el sistema binario y la notación del desplazamiento:
Algoritmo recursivo
Este problema se suele plantear a menudo en programación, especialmente para explicar la recursividad. Si numeramos los discos desde 1 hasta n, si llamamos origen a la primera pila de discos, destino a la tercera y auxiliar a la intermedia, y si a la función la denomináramos Hanói, con origen, auxiliar y destino como parámetros, el algoritmo de la función sería el siguiente:

Solución iterativa
Para obtener la solución más corta, es necesario mover el disco más pequeño en todos los pasos impares, mientras que en los pasos pares sólo existe un movimiento posible que no lo incluye. El problema se reduce a decidir en cada paso impar a cuál de las dos pilas posibles se desplazará el disco pequeño. El algoritmo en cuestión depende del número de discos del problema:
- Si inicialmente se tiene un número impar de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila destino, y en cada paso impar se le mueve a la siguiente pila a su izquierda (o a la pila destino si está en la pila origen). La secuencia será: destino, auxiliar, origen, destino, auxiliar, origen, etc.
- Si se tiene inicialmente un número par de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila auxiliar, y en cada paso impar se le mueve a la siguiente pila a su derecha (o a la pila origen si está en la pila destino). La secuencia será: auxiliar, destino, origen, auxiliar, destino, origen, etc.
Una forma equivalente de resolverlo es coloreando los discos pares de un color y los impares de otro, y se resuelve el problema añadiendo la siguiente regla: no colocar juntos dos discos de un mismo color. De esta manera, solo queda un movimiento posible (además del de volver hacia atrás).
Grafos de Hanói
Se llama grafo a un conjunto de puntos que se unen entre sí mediante líneas que siguen reglas fijadas para cada caso. Los puntos se denominan vértices y las líneas aristas que pueden estar o no orientadas. Se dice que un vértice es par si en él incide un número par de aristas. En el otro caso se dice que es impar.
Con respecto a los grafos de las Torres de Hanói, existe una conexión con el Triángulo de Sierpinski. Mediante la teoría de grafos, el profesor Ian Stewart de The University of Warwick (Inglaterra), indica que cada serie tiene una única configuración. El grafo sigue una configuración similar a un triángulo equilátero cuyos vértices contienen varios triángulos colocados en su interior. Cada lado de un triángulo pequeño representa un movimiento del disco pequeño, cada lado de un triángulo mediano que no pertenezca a un triángulo pequeño representa un movimiento del disco segundo y cada lado del triángulo grande que no pertenezca a un triángulo menor representa los movimientos del disco grande. Este gráfico representa todos los posibles movimientos para la solución y cuando se incrementa el número de discos, el gráfico se convierte en un fractal. Cada una de sus partes reproduce el modelo del grafo completo. Por ejemplo para 3 discos se tiene el grafo:
Los códigos del grafo representan cada movimientos, tal como se muestra en el gráfico:
El camino más corto - la ruta de los monjes
Al representar los posibles movimientos en un grafo, siempre tendremos que la diagonal del costado derecho nos guiará por el mínimo número de movimientos, desde la varilla A (origen) hasta la varilla C (destino). Tenemos por ejemplo la representación del grafo para 3 discos, que resultan 2³-1=7 movimientos, guiado por la línea anaranjada desde la A (punto verde) hasta la varilla C (punto rojo).
Teniendo en cuenta la leyenda, Brahma había colocado 64 discos, el número de movimientos por la “ruta de los monjes” es igual a 2⁶⁴-1, hecha la operación resulta 18.446.744.073.709.551.615 movimientos, entonces ¿cuánto tiempo tardarán los monjes en cumplir el mandato de Brahma? Supongamos que no se equivocan y cada movimiento se realiza en un segundo, eso resultaría 584.942.417.352 años, tiempo calculado para el fin del mundo.
El camino más largo
Se puede elegir un camino que recorra todas las situaciones posibles del juego y, por tanto, todos los puntos y códigos posibles. Para encontrar dicho camino debemos recorrer todo el grafo sin pasar dos veces por el mismo vértice y se tendrá 3ⁿ - 1 movimientos.
La forma de encontrar el camino más largo en este grafo es recurrente y se puede encontrar de manera sencilla si recorremos los siguientes pasos:
i) Si n es par recorremos el primer triángulo pequeño en sentido horario. Si n es impar lo recorremos en sentido anti horario.
ii) Pasamos al único triángulo pequeño accesible desde el fin del recorrido anterior y lo recorremos en el sentido contrario al anterior.
iii) Repetimos el paso ii tantas veces como sea necesario hasta llegar a la última posición.
La representación para tres discos se tiene 3ᶟ - 1 = 26 movimientos posibles, como se muestra en el grafo, guiado por la línea anaranjada:
Grafos Hanói según el número de discos:
En programación
En la informática y la introducción a la teoría de algoritmos el juego de las torres de Hanói, se emplea como ejemplo de recursividad por excelencia. Un ejemplo en el lenguaje C es:
#include <stdio.h>
#include <conio.h>
void hanoi(int n,int com, int aux, int fin);
void main(void){
clrscr();
char com=’A’;
char aux=’B’;
char fin=’C’;
int n;
printf(“\número de discos: “);
scanf(“%d”,&n);
fflush(stdin);
printf(“\n\nLos movimientos a realizar son: \n”);
hanoi(n,com,aux,fin);
}
void hanoi(int n,int com, int aux, int fin){
if(n==1){
printf(“%c->%c”,com,fin);
}
else{
hanoi(n-1,com,fin,aux);
printf(“\n%c->%c\n”,com,fin);
hanoi(n-1,aux,com,fin);
}
En otros lenguajes...
El juego:
Fuentes: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.



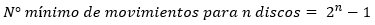






Este comentario ha sido eliminado por el autor.
ResponderEliminarfabuloso
ResponderEliminar