DIAGRAMA DE DISPERSIÓN

 

 

El gráfico de dispersión, también conocido como diagrama de dispersión, gráfico de correlación, nube de puntos, diagrama XY, scatter plot, scatter chart o scattergram; es una herramienta gráfica estadística que se usa para visualizar la relación que existe entre dos variables cuantitativas, representadas mediante puntos de datos distribuidos en un plano cartesiano; este gráfico es muy útil para detectar patrones, tendencias y correlaciones, ya sean positivas, negativas o inexistentes, que pueden producirse entre dos variables. El gráfico de dispersión en combinación con el coeficiente de correlación de Pearson, aportan información muy útil al análisis de datos, explica cómo afecta una variable a la otra y permite identificar problemas para tomar ciertas acciones y mejorar los procesos.

Elementos del Diagrama de Dispersión:

1. Ejes X y Y. Representan las 2 variables cuantitativas que se comparan; el eje X suele representar la variable independiente; en tanto que el eje Y representa la variable dependiente.
2. Puntos de datos. Cada punto del gráfico representa un par de valores (x, y) de las variables que se están analizando; cada punto es una observación individual del conjunto de datos.
3. Título y etiquetas. Incluyen el título del gráfico y las etiquetas de los ejes para describir las variables representadas.
4. Escala de los ejes. Los ejes X y Y deben incluir rangos de valores que permitan interpretar adecuadamente los puntos de datos.
5. Puntos atípicos (outliers). Son puntos que se alejan o que se desvían significativamente del patrón general que sigue el resto de los datos.
6. Línea o curva de tendencia (opcional). Para mejorar la visualización de la relación entre las variables a veces incluimos una línea o una curva de tendencia que muestre la dirección los datos (p.e. una línea de regresión).

 

Objetivos del diagrama de dispersión:

- Determinar la relación existente entre las dos variables; la relación puede ser positiva (a medida que una variable crece la otra también crece), negativa (a medida que una variable crece la otra disminuye) o inexistente (no se observa una tendencia o patrón claro de relación).
- Detectar patrones y tendencias en los datos, que pueden ser lineales o no lineales, lo que resulta útil para anticipar comportamientos futuros o bien, para modelar relaciones matemáticas.
- Representar visualmente grandes conjuntos de datos de forma sencilla y comprensible, de manera que analistas y científicos puedan comunicar hallazgos complejos de forma clara y efectiva.
- Identificar valores atípicos (outliers), es decir, aquellos valores que se desvían significativamente del patrón general y entonces examinarlos en el conjunto de datos para realizar análisis posteriores
- Evaluar la intensidad y la dirección de una relación entre las dos variables, con la finalidad de validar hipótesis y teorías.


Limitaciones del diagrama de dispersión:

- Los gráficos de dispersión sólo pueden mostrar la relación entre dos variables a la vez, lo que resulta limitante cuando se quiere analizar la interacción entre más de dos variables.
- En conjuntos de datos muy grandes, los gráficos de dispersión pueden quedar desbordados o abarrotados y ser difíciles de leer ya que los puntos pueden superponerse unos a otros, dificultando la identificación de patrones y tendencias claras.
- Es sensible a escalas y rangos de los ejes, si las escalas no son las adecuadas, puede alterar la interpretación visual de los datos, llevando a conclusiones erróneas sobre la relación entre las variables.
- Los gráficos de dispersión muestran correlaciones entre las variables, pero no establecen causalidad; las variables pueden estar correlacionadas sin que una cause a la otra.
- Influencia de valores atípicos u outliers, unos cuantos puntos de datos extremos podrían influir significativamente en la percepción de la tendencia general.


Pasos para la creación de un Diagrama de Dispersión:

1. Definir la situación y determinar las variables a estudiar (de las cuales queremos saber la relación).
2. Recolectar los datos de las variables, entonces, las dos variables deben estar dados en el mismo periodo de tiempo y deben tener la misma cantidad de datos muestrales.
3. Preparar los datos en un formato adecuado generalmente en una hoja de cálculo con una columna para cada variable, limpiar los datos eliminando valores faltantes o incorrectos
4. Seleccionar un software o herramienta que se utilizará para la creación del gráfico, podría ser Excel, R, Python, SPPS, etc.
5. Crear el diagrama de dispersión en el software elegido (en R usar la función plot() y en Python plt.scatter() con mathplotlib).
6. Personalizar el diagrama etiquetando ejes, agregando títulos, ajustando escalas, añadiendo línea de tendencia, o cualquier ajuste según la necesidad.
7. Analizar los puntos de datos para identificar patrones, tendencias o correlaciones, además de los valores atípicos.
8. Determinar el coeficiente de correlación, puede existir una correlación positiva, negativa o ninguna relación entre las variables.
9. Y finalmente documentar los hallazgos y tomar las decisiones pertinentes.

Interpretación del Diagrama de Dispersión:

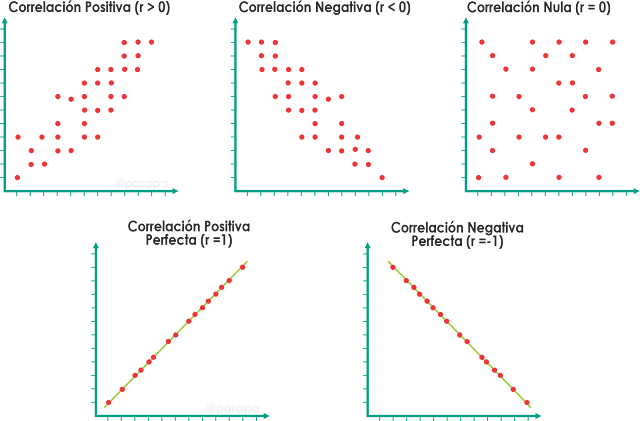
- Correlación positiva, cuando una variable aumenta, la otra también lo hace, es decir que gráficamente los puntos tienden a ascender de izquierda a derecha, lo que indica que las variables tienen una relación directa.
- Correlación negativa, cuando una variable aumenta, la otra disminuye; si los puntos tienden a descender de izquierda a derecha, indica que las variables tienen una relación inversa.
- Correlación nula o sin correlación, cuando no hay una relación aparente entre las variables, gráficamente, los puntos se encuentran dispersos sin un patrón claro.

- Correlación lineal y no lineal: Los diagramas de dispersión revelan si la relación entre las variables es lineal (una línea recta) o no lineal (una curva, p.e. exponencial, parabólica, etc).

- Fuerza de la correlación, los valores pueden estar correlacionados de manera fuerte, débil o nula y puede ser positiva o negativa.

 

 

El coeficiente de correlación en un diagrama de dispersión

El coeficiente de correlación cuantifica la relación entre dos variables y se puede representar en un diagrama de dispersión, el coeficiente de correlación de Pearson (𝑟) es el más utilizado. Para determinar la fuerza y la dirección entre dos variables, el coeficiente de correlación lineal se calcula mediante el cociente entre la covarianza de las dos variables y el producto de sus desviaciones típicas, de la siguiente forma:

El valor de este coeficiente se encuentra entre −1 y 1, cuanto más próximo a 1, la correlación será fuerte y positiva, y cuanto más cercano a -1, la correlación será fuerte y negativa; si el valor es próximo a 0, la correlación será débil.


Por último, el gráfico de dispersión permite de tomar decisiones a partir de sus formas visuales y comprender la relación que existe entre dos variables cuantitativas; además, su utilidad y efectividad a la hora de presentar datos lo convierten en una herramienta muy utilizada e importante para comunicar la información.

Referencia:(1), (2), (3), (4), (5).